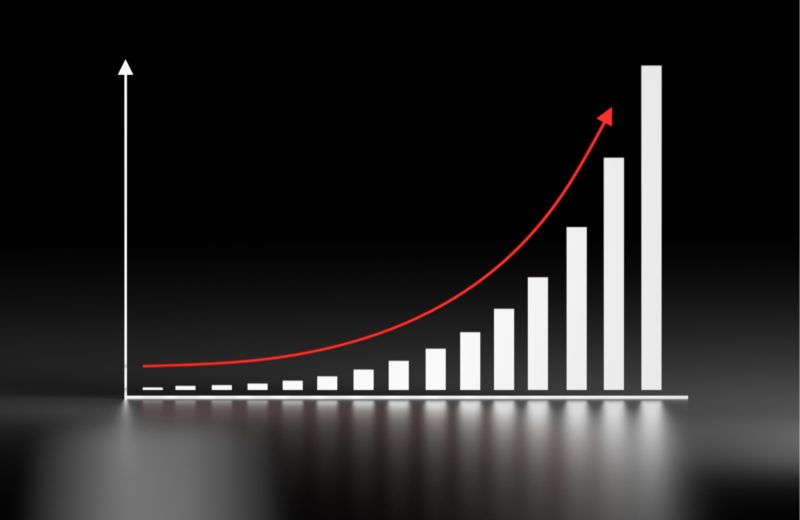
Why Exponential Predictions are Always Wrong - Population, Technology and Resources
I’ve written on the ways that cognitive bias can derail rational thinking, but there’s another major pathway to error — we get the numbers wrong. One of the biggest mistakes is to believe in exponential trends. An exponential trend is one that increases by a set percentage each time period – this does not sound particularly dangerous until you factor in the compounding effect.

Consider the following parable: A master was pleased with his servant and asked what he would wish for. The servant asked for rice – one grain on the first square of a chessboard, two on the second, four on the third, and so on. This is exponential compounding. The master thought this was a reasonable request and began to count out the rice – only to find that the number required was more than the entire harvest. The number required would be 2^63 – actually quite a bit larger than the number of atoms comprising the entire earth.
Exponential Growth of the Human Population
Adam Kucharski, in his recent Nautilus article “How Many Humans Can the Earth Support”, traces the problem with exponential population forecasting back to Robert Malthus. In 1798, Malthus forecast that England’s population would double every twenty-five years, following an exponential growth trend that would quickly outstrip food production and lead to disaster. The forecast failed to materialize, as did the disaster, for two reasons. First, the population growth rate slowed, but, more importantly, innovation resulted in significant increases in the capacity of England to sustain its population.

Human population growth is one measure of change in an extraordinarily complex dynamic system that involves millions of family units and a constantly evolving system of food production and distribution, among other economic and demographic factors. It is also subject to constraints – such as food – that will curtail or stop population growth unless that constraint can be mitigated. While the population may grow exponentially for a period, that growth will inevitably slow down in the face of constraints. It is ludicrous to think the population will grow exponentially forever.
But the power of exponential thinking to capture the human imagination is as strong today as it ever was, and there have been continuing arguments that exponential population growth would exceed fixed resource capacities, leading to disaster. One of the most popular was The Population Bomb (1968) by Paul R. Ehrlich. The imminent disaster has so far failed to materialize, for the same reasons that applied to Malthus’ forecast. Population growth has slowed. In fact, in some industrialized nations population growth has dropped below the replacement rate — population decline is now a larger concern. In addition, human ingenuity and innovation have continued to increase the available food supply. The current global population of 7.5B is better fed, on average than at any time in the past.
Exponential Growth in Computer Technology
The latest exponential narrative capturing the human imagination is that computer capabilities are growing exponentially and will soon lead to an explosion of machine intelligence. The basis for this forecast is “Moore’s Law”, an observation made in 1965 by Intel’s founder Gordon Moore that computer capacity and memory were doubling about every 18 months – a trend which continued unabated for nearly five decades. Building on that trend, the supposed “singularity,” according to Ray Kurzweil’s The Singularity is Near (2005), will involve super intelligence of relatively infinite capacities (compared to our own). The need for human labour will end and human health limitations will be eliminated – physical immortality will be a reality.
Of course, Moore’s law has finally begun to slow. Computer technology is reaching hard limits in size and complexity. In addition, both Artificial Intelligence and human longevity are proving remarkably difficult to achieve. Ten years out, it seems we are no closer to the singularity than we were in 2005. That is the nature of complex systems – we should not be fooled by claims of exponential growth.
Exponential Growth in Human Resource Consumption
One more exponential growth trend we should be very concerned about – human resource consumption. We tend to focus on the question of population growth. But here is an interesting fact. The worldwide population has increased by nearly a factor of 10 in the last hundred years, to 7.5 Billion, and has a ways to go yet before stabilizing. But at the same time, the global production of goods and services, measured as average per capita GDP, has also increased by about ten-fold. This means the total production of all goods and services in our global economies has increased almost one hundred times in a century – ten times faster than population growth.
Can this extraordinary exponential growth possibly continue? Of course not. But, if our expectations for the future rely on the assumption of continued growth in consumption as the basis for human thriving, we are going to be badly disappointed. Malthus and Ehrlich were right about this: Populations that grow quickly past available resources are subject not to stabilization, but to collapse. This is what happens to a bacteria colony growing in a petri dish.

The key question now is when the immense growth in resource consumption of the past century becomes (or became) unsustainable. The corollary question is how massive the collapse will be for different components of the system that are now under stress. The final question is – what are we going to do about it?